Notes by Michael K. Pellegrino
Class #1 - Tuesday, July 10, 2012
Incidence Axiom I - Given any two disticnt points, P and Q, there exists exactly one line L such that P and Q lie on L.
Incidence Axiom II - For every line L there exists at least two distinct points, P and Q, such that both P and Q lie on L.
Incidence Axiom III - There exist three points that do not lie on any one line.
Colinear - Three points A, B, and C are colinear if there exists a line L such that all three points lie on L
Non-colinear - Three points A, B, and C are non-colinear if there does not exist a line L such that all three points lie on L
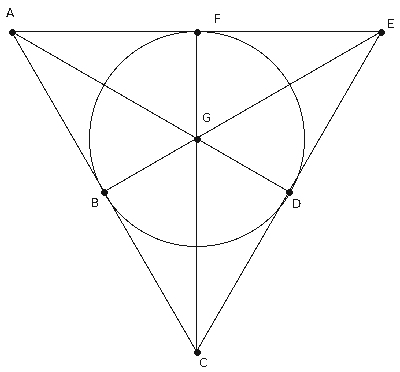
Fano's Geometry
Interpret Point to be one of A, B, C, D, E, F, and G
Interpret Line to be one of the seven triples: (ABC), (CDE), (EFA), (AGE), (CGF), (EGB) and (BDF)

Do all three incidence axioms work for this geometry? yes.
An interpretation of an axiomatic system is a particular/specific way of giving meaning to the undefined terms in the system.
Interpretation is a model if the axioms are all true in that interpretation.
| Axiom I | Axiom II | Axiom III |
|---|---|---|
| Given any 2 distinct pts, there exists exactly 1 line | For every line there exists at least 2 distinct pts | There exist 3 pts that do not lie on any 1 line |
| True | True | True |
A statement in our axiomatic system is independent of the axioms if it cannot be proven or disproven as a logical consequence of the axioms.
If we can make 2 models up, where in one of which, the statement is true and in the other of which the statement is false, then we know the statement is independent of the axioms.
Definition 2.3.1: Parallel - Two lines L and M are said to be parallel if they lie in the same plane and there is no point P such that P lies on both L and M. Symbolically written: L || M.
Euclidian Parallel Postulate - For every line L and for every point P not on L there is exactly one line M such that P lies on M and M || L.
Elliptic Parallel Postulate - For every line L and for every point P not on L there is no line M such that P lies on M.
Hyperbolic Parallel Postulate - For every line L and for every point P not on L there are at least two lines M and N such that P lies on M and N and M || L and N || L.
Concerning Spheres
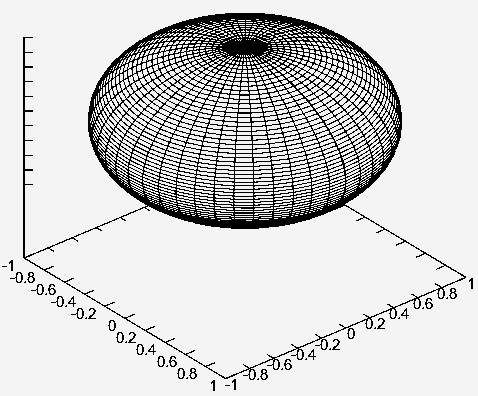
Interpret point to be an ordered triple of real numbers (x, y, z) with x² + y² + z² = 1
Interpret line to be a Great Circle on a sphere. (A Great Circle is a circle whose radius is the radius of the sphere.)
The intersection of the plane that passes through the origin (0, 0, 0) and the two points involved on the sphere with the sphere.
The two points on the sphere are said to be Antipodal (opposite) if they are points on which a line through the origin intersects the sphere.
Two given antipodal points on the sphere lie on an infinite number of Great Circles.
Incidence Axiom I is NOT satisfied using two antipodal points on a sphere so this is NOT a model for incidence geometry.
It does however satisfy the elliptic parallel postulate.
Five Point Geometry
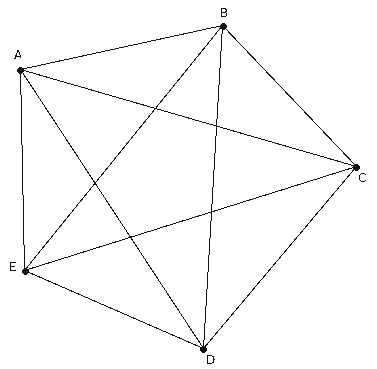
Interpret points to be one of A, B, C, D and E
Interpret line to mean a set of exactly two points.
| Axiom I | Axiom II | Axiom III |
|---|---|---|
| Given any 2 distinct pts, there exists exactly 1 line | For every line there exists at least 2 distinct pts | There exist 3 pts that do not lie on any 1 line |
| True | True | True |
Also, Hyperbolic Parallel Postulate holds because for every line L and for every point where P=A,B,C,D or E not on L, there are at least two lines M and N such that P lies on M and P lies on N.
Four Point Geometry
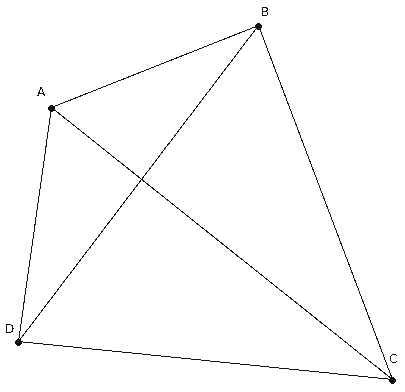
Interpret point to be one of A, B, C or D.
Interpret line to be a set of two points.
| Axiom I | Axiom II | Axiom III |
|---|---|---|
| Given any 2 distinct pts, there exists exactly 1 line | For every line there exists at least 2 distinct pts | There exist 3 pts that do not lie on any 1 line |
| True | True | True |
Also, Euclidean Parallel Postulate holds because for every line L and for every point P not on L there is exactly one line M such that P lies on M and M || L.
Three Point Geometry
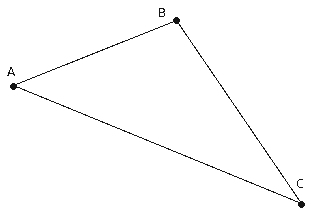
Interpret point to be one of A, B or C.
Interpret line to be a set of two points.
| Axiom I | Axiom II | Axiom III |
|---|---|---|
| Given any 2 distinct pts, there exists exactly 1 line | For every line there exists at least 2 distinct pts | There exist 3 pts that do not lie on any 1 line |
| True | True | True |
Also, Elliptic Parallel Postulate holds because for every line L and for every point P not on L there is no line M such that P lies on M.
Two Point Geometry

Interpret point to be one of A or B.
Interpret line to be a set of two points.
| Axiom I | Axiom II | Axiom III |
|---|---|---|
| Given any 2 distinct pts, there exists exactly 1 line | For every line there exists at least 2 distinct pts | There exist 3 pts that do not lie on any 1 line |
| True | True | False |
This is not incidence geometry because it doesn't satisfy Axiom III.
Theorem 2.5.1 - Lines that are NOT Parallel intersect in exactly one point in a plane.
Proof - Let L and M be two distinct lines in the same plane that are not parallel.
L and M must intersect in at least one point P (by the definition of parallel). If L and M are parallel then there is no point R such that R lies in both L and M.
P → Q
NEGATION - if P → Q is NOT true then there is a point R such that R is on both L and M.
If L and M are not parallel then there is a point R such that R is on both L and M.
R.A.A. - Reductio ad absurdium - Proof by contradiction.
Suppose lines L and M intersect in two points R and S then the points R and S are both on line L... this violates Incidence Axiom I. This contradiction means that lines L and M cannot intersect in more than one point hence L and M are distinct, non-parallel lines and they must intersect in exactly one point.
Converse - if Q is true then P is true. Q → P?
If L and M intersect in exactly one point then L and M are distinct and non-parallel.
In this case, the converse is indeed true, but this is not always the case.
Proof: Suppose L = M then there exists exactly one point R that lies on both L and M (given). Incidence Axiom II says that L must contain two points R and S. Since L is supposed to equal M then R and S would have to lie on both L and M. This last statement contradicts Incidence Axiom II hence L must NOT be equal to M. We are given that L and M intersect so that means that they are not parallel.
Contrapositive - if P → Q then !Q → !P is also true.
This is because of the following truth tale:
| P | Q | !P | !Q | P → Q | !Q → !P |
|---|---|---|---|---|---|
| T | T | F | F | T | T |
| T | F | F | T | F | F |
| F | T | T | F | T | T |
| F | F | F | T | T | T |
Theorem - if x = 0 then x² = 0
Contrapositive - if x2 ≠ 0 then x ≠ 0
Converse - if x2 = 0 then x = 0
Contrapositive of the Converse - if x ≠ 0 then x2 ≠ 0
Conditional Statements - if P is true then Q is true (P → Q). P is the hypothesis and Q is the conclusion.
A theorem is a conditional statement that has been proven to be true.
If A ≠ 0 then A2 ≠ 0 (a conditional statement)
This is not a theorem for matrices because there is a counter example
Once a theorem has been formed (meaning it's been proved to be true) we can write P ⇒ Q
Example: If x is in ℝ and x2 < 0 then x = 4
Note... the conclusion is true for all x for which the hypothesis is true.
There happen to not be any x's for which the hypothesis is true, so there are no counterexamples to this theorem. It is true... but we say that this theorem is vacuously true.
It's like saying that all cell phones in the room are turned off when there aren't any cell phones in the room. All of them ARE off, but all the cell phones in the room are also on because there aren't any cell phones. So one could also say that "All the cell phones in the room are on and off" because of the vacuous nature of this truth.
Example: If x is irrational then x2 is irrational. This is false because √2 is irrational, but (√2)2 = 2 which is rational.
THEOREM 2.6.3 - If L is any line then there exists at least one point P such that P does not lie on L. (Assume Incidence Geometry).
PROOF - Let L be any line then there are three points (A, B and C) that are non-colinear (Incidence Axiom III)
Hence at least one of them doesn't lie on L
THEOREM 2.6.4 - If P is any point there are at least two distinct lines L and M such that P lies on both L and M
PROOF - Let P be any point. By Incidence Axiom III there exist three non-colinear points A, B and C.
Case 1: P is one of those three points
P = A
L = Line AB and M = Line AC (by Incidence Axiom I)
P=A lies on both of these lines
Suppose L = M... this is not possible because they'd have to be co-linear so L ≠M and the theorem is true. It follows Without Loss Of Generality the same if P=B or P=C
Case 2: Suppose P is NOT one of these points.
Let L = line PA, M = line PB and N = line PC (by Incidence Axiom I)
These three lines cannot be the same because that would imply that A, B and C are co-linear... hence at least two of the three lines are distinct and P lies on both of those.
Class #2 - Thursday, July 12, 2012
Chapter 3
Cenema's Axioms for Two Dimenstional Plane Geometry
Axiom 3.1.1 - Existance Postulate - the set of all points is a non-empty set with at least two points
The set of all points is called the Plane and denoted P
A line through the points A and B is denoted by AB with a double-arrowed line over it.
We write A in L to indicate the point A lies on the line L, or a is incident with L
Axiom 3.1.3 - Incidence Postulate - Every line is a set of points where every pair of distinct points (A and B) is exactly one line L on AB such that A and B are incident with L. A, B in L
A point Q is extetrnal to L if Q is not incident with L
Two lines L and M are parallel if they lie in the same plane and there is no point P with P on L and P on M. L || M or L AND M = NULL
Theorem 3.1.7: if L and M are two distinct non-parallel lines then there exists exactly one point P that lies on both L and M.
Corollary - If L and M are lines, the three possibilities are that: L=M, L||M, or L AND M contains exactly one point.
Axiom 3.2.1 - Ruler Postulate - for every pair of points (P and Q) there exists a real number ℝ. PQ ≡ ||PQ|| is the distance from P to Q and there exists a line L. There is a 1:1 mapping
F:l → ℝ such that if P and Q are points on the line corresponding to the x,y in ℝ, x = f(P) and y = f(Q), then we're claiming that the distance from P to Q is PQ=||x-y||.
Let L be a line, a 1:1 correspondence (meaning a function that is 1:1 and onto) f:l → ℝ such that PQ = |f(P) - f(Q)| for all points PQ in L is called a coordinate function for L and the number f(P) is called the coordinate of P.
Def: Let A,B,C be distinct points. We say that B is between A and C and write A*B*C if A, B, and C are colinear. C ∈ AB and AB + BC = AC. Also f(A) < f(B) < f(C) or f(C) < f(B) < f(A). It turns out that if AB + BC = AC for three distinct points in a plane A, B, and C need to be colinear. In general AB + BC > AC (The Triangle Inequality).
The segment joining A and B in AB: AB = { A, B } U { P | A*P*B }. A in f(A), B in f(B) with A < B. [A,B] = { x | A < X < B is AB> is the ray from A in the direction of B. AB U { P | A * B * P }
Def: the Length of AB denoted by AM is the distance from A to B.
We call A and B the endpoints of AB and two segments AB and CD are congruent if AB = CD